Project / DeepLearningFromForR7 minutes read (About 1073 words)

순전파를 사용하여 모델 학습하기


순전파법을 사용하여 손글씨 추론 모델을 만들어보겠습니다. 순전파법의 기본 원리는 손실함수 값을 최소화 시키는 것입니다. 손실함수 값을 최소화 시키는 방법으로는 경사하강법(SGD)를 사용합니다. 순전파의 기본 설명은 다음 링크를 참고하세요.

먼저, 학습할 네트워크를 만듭니다. W1,W2는 각 층별 가중치이며 b1,b2는 편향 값을 의미합니다.

1
2
3
4
5
6
7
8
TwoLayerNet <- function(input_size, hidden_size, output_size, weight_init_std  =  0.01) {
  W1 <- weight_init_std * matrix(rnorm(n  =  input_size*hidden_size), nrow  =  input_size, ncol  =  hidden_size)
  b1 <- matrix(rep(0,hidden_size), nrow = 1, ncol = hidden_size)
  W2 <- weight_init_std * matrix(rnorm(n  =  hidden_size*output_size), nrow  =  hidden_size, ncol  =  output_size)
  b2 <- matrix(rep(0,output_size),nrow = 1, ncol = output_size)
  
  return (list(W1 = W1, b1 = b1, W2 = W2, b2 = b2))
}

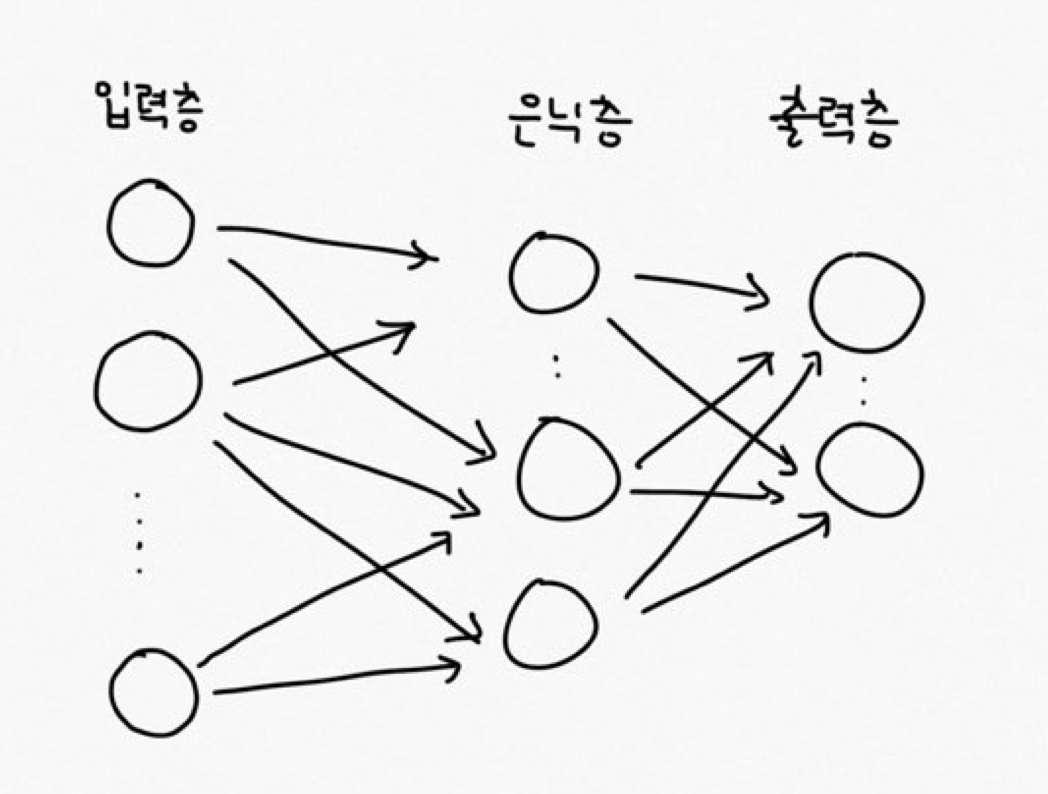
TwoLayerNet 네트워크는 아래와 같이 은닉층을 1개 갖습니다.

입력층에서 input_size 개수만큼의 노드를 갖고 은닉층에서는 hidden_size 개수만큼의 노드, 출력층에서는 output_size만큼의 노드를 갖습니다. W1과 b1은 입력층에서 은닉층으로 갈 때의 가중치와 편향이며 W2와 b2는 은닉층에서 출력층으로 갈 때 사용하는 가중치와 편향입니다. 그리고 weight_init_std는 가중치 초기값이 큰 값이 되는 것을 방지하는 파라미터입니다.

다음으로, 데이터를 불러오고 트레이닝 셋과 테스트 셋으로 분류합니다. 데이터는 MNIST 라이브러리의 손글씨 이미지입니다. R에서는 dslabs를 임포트합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
library(dslabs)
source("./functions.R")
source("./utils.R")
source("./model.R")

init <- function(){
  mnist_data <- get_data()
  #손글씨 데이터
  x_train_normalize <<- mnist_data$x_train 
  x_test_normalize <<- mnist_data$x_test
  #정답 레이블
  t_train_onehotlabel <<- making_one_hot_label(mnist_data$t_train,60000, 10)
  t_test_onehotlabel <<- making_one_hot_label(mnist_data$t_test,10000, 10)
}

손실함수는 교차엔트로피오차 함수를 사용합니다. 교차엔트로피오차 함수는 아래와 같이 구현합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
model.forward <- function(x){
  z1 <- sigmoid(sweep((x %*% network$W1),2, network$b1,'+'))
  return(softmax(sweep((z1 %*% network$W2),2, network$b2,'+')))
}

cross_entropy_error <- function(y, t){
    delta <- 1e-7
    batchsize <- dim(y)[1]
    return(-sum(t * log(y + delta))/batchsize)
}

loss <-function(x,t){
  return(cross_entropy_error(model.forward(x),t))
}

기본 교차엔트로피 함수식에 delta값을 추가하였는데, 이는 log0이 되면 -Inf가 되는 문제를 방지하기 위해서 입니다.

다음으로 경사하강법은 손실함수 값을 최소화 시키기 위해 사용합니다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
numerical_gradient_W <- function(f,x,t,weight){
    h <- 1e-4
    vec <- matrix(0, nrow = nrow(network[[weight]]) ,ncol = ncol(network[[weight]]))
    for(i in 1:length(network[[weight]])){
        origin <-  network[[weight]][i]
        network[[weight]][i] <<- (network[[weight]][i] + h)
        fxh1 <- f(x, t)
        network[[weight]][i] <<- (network[[weight]][i] - (2*h))
        fxh2 <- f(x, t)
        vec[i] <- (fxh1 - fxh2) / (2*h)
        network[[weight]][i] <<- origin
    }
    return(vec)
}

numerical_gradient <- function(f,x,t) {
  grads  <- list(W1 = numerical_gradient_W(f,x,t,"W1"), 
                 b1 = numerical_gradient_W(f,x,t,"b1"), 
                 W2 = numerical_gradient_W(f,x,t,"W2"), 
                 b2 = numerical_gradient_W(f,x,t,"b2"))
  return(grads)
}

마지막으로 학습시키는 함수입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
train_model <- function(batch_size, iters_num, learning_rate, debug=FALSE){
  #seperate train, test data
  init()
  train_size <- dim(x_train_normalize)[1]

  iter_per_epoch <- max(train_size / batch_size)
  for(i in 1:iters_num){
    batch_mask <- sample(train_size,batch_size)
    x_batch <- x_train_normalize[batch_mask,]
    t_batch <- t_train_onehotlabel[batch_mask,]

    grad <- numerical_gradient(loss, x_batch, t_batch)
    network <<- sgd.update(network,grad,lr=learning_rate)

    if(debug){
        if(i %% iter_per_epoch == 0){
            train_acc <- model.evaluate(model.forward, x_train_normalize, t_train_onehotlabel)
            test_acc <- model.evaluate(model.forward, x_test_normalize, t_test_onehotlabel)
            print(c(train_acc, test_acc))
        }
    }

    train_accuracy = model.evaluate(model.forward, x_train_normalize, t_train_onehotlabel)
    test_accuracy = model.evaluate(model.forward, x_test_normalize, t_test_onehotlabel)
    return(c(train_accuracy, test_accuracy))
    }
}

train_model()함수 중간에 sg.update()함수는 경사하강법으로 변경된 가중치를 업데이트하는 역할을 합니다.
코드는 아래와 같습니다.

1
2
3
4
sgd.update <- function(network, grads, lr = 0.01){
  for(i in names(network)){network[[i]] <- network[[i]] - (grads[[i]]*lr)}
  return(network)
}

이제 모든 준비를 마쳤습니다. 네트워크를 생성한 후 모델을 학습시켜봅니다.

1
2
network <<- TwoLayerNet(input_size = 784, hidden_size = 50, output_size = 10)
train_model(100, 10000, 0.1, TRUE)
#

Comments

×