Project / DeepLearningFromForR11 minutes read (About 1615 words)

딥러닝에 쓰이는 함수를 R과 Python으로 구현하기


딥러닝 책 『밑바닥부터 시작하는 딥러닝』 을 공부하면서, 책에 있는 Python코드를 R로 구현하는 프로젝트를 진행하고 있습니다.

Python으로 구현한 딥러닝 함수 코드와 R로 구현한 함수 코드를 동시에 살펴 보고자 합니다.

1. 시그모이드(Sigmoid) 함수

시그모이드 함수는 활성화 함수역할을 하는 대표 함수입니다.
함수 식은 다음과 같습니다.

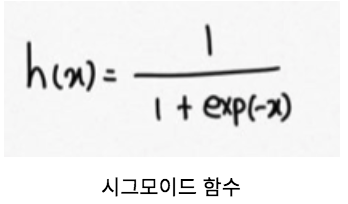
파이썬의 경우, Numpy의 지수함수인 exp()를 사용해서 구현합니다.

1
2
def sigmoid(x):
    return 1/ (1+np.exp(-x))

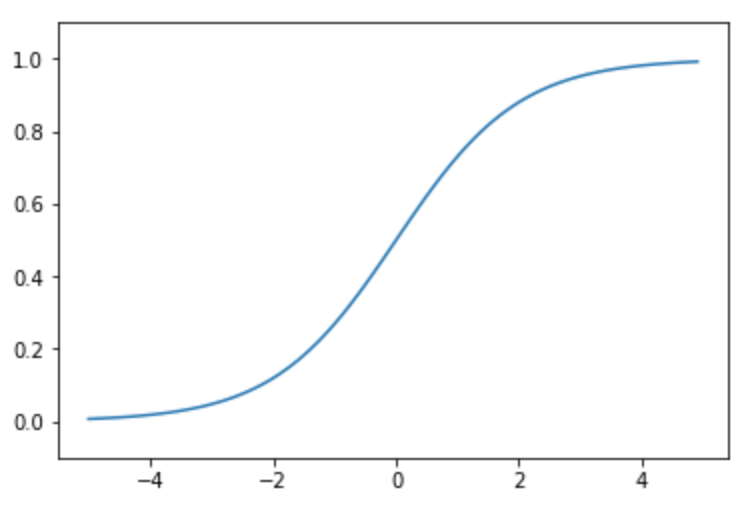
시그모이드 함수를 그래프로 나타내기 위해 임의의 x값을 정하고 matplotlib으로 나타냅니다.
여기서 x는 [-5.0, -4.9, -4.8, …. 4.9]가 됩니다.

1
2
3
4
5
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

R은 행렬 계산을 기본으로 하기 때문에 다른 라이브러리를 임포트할 필요 없이 exp()를 사용할 수 있습니다.

1
2
3
4
sigmoid <- function(x)
{
    return(1 / (1 + exp(-x)))
}

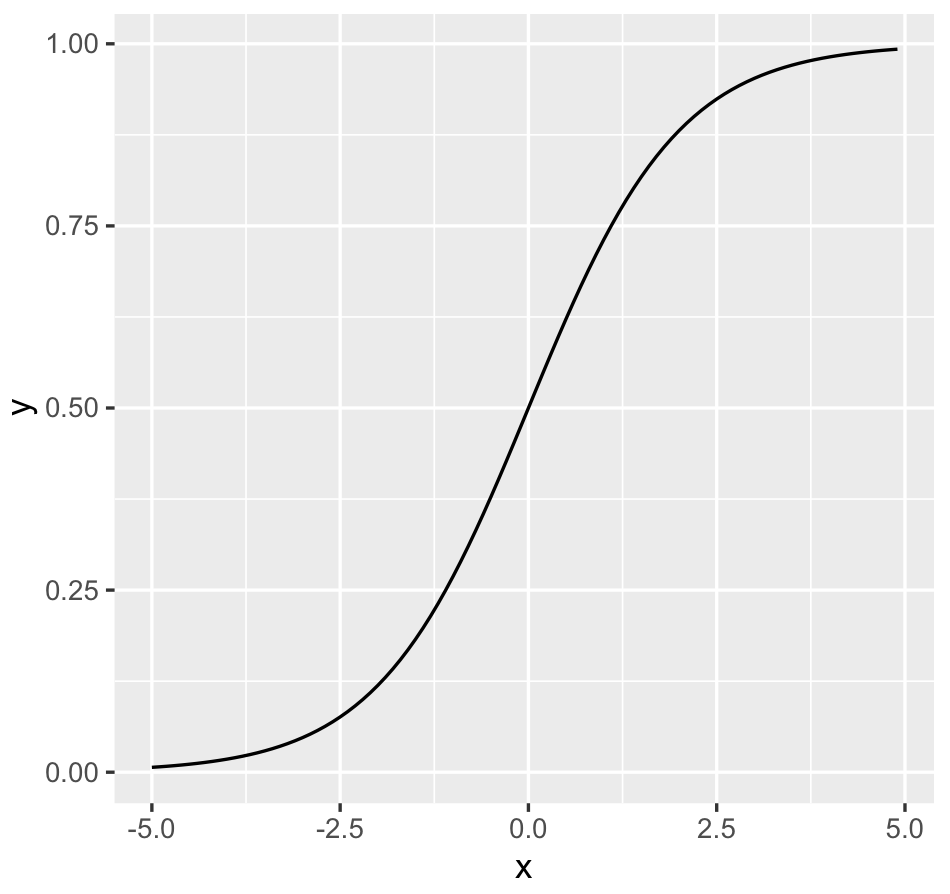
마찬가지로, 임의의 x값을 정하고 ggplot2 라이브러리로 그래프를 그립니다.

1
2
3
4
5
6
7
library(ggplot2)

x <- seq(from =  -5, to =  4.9, by =  0.1)
y <- sigmoid(x)
data <- data.frame(x, y)

ggplot(data, aes(x, y)) + geom_line()

2. 렐루(Relu) 함수

렐루 함수 역시 마찬가지로 활성화 함수의 대표 함수 중 하나입니다.
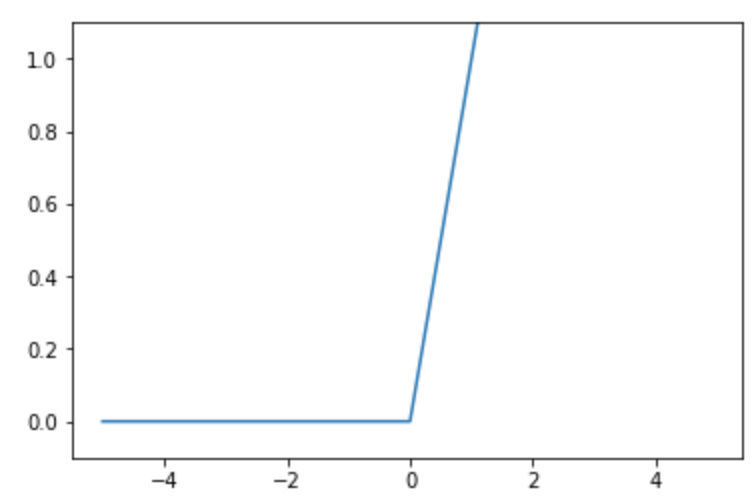
시그모이드 함수와의 차이점은 임계점을 기준으로 0 또는 입력 값을 출력한다는 것입니다.

1
2
3
4
5
6
7
8
def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

R도 간단하게 구현합니다.

1
2
3
4
5
6
7
8
9
relu <- function(x)
{
    return(ifelse(x > 0, x, 0))
}

x <- seq(from = -5, to = 4.9, by = 0.1)
y <- relu(x)
data <- data.frame(x, y)
ggplot(data, aes(x, y)) + geom_line()

아래의 결과를 보면 0보다 작은 x값에 대해서는 결과값이 0 이고, 0보다 큰 x값에 대해서는 x값을 출력하고 있음을 확인할 수 있습니다.

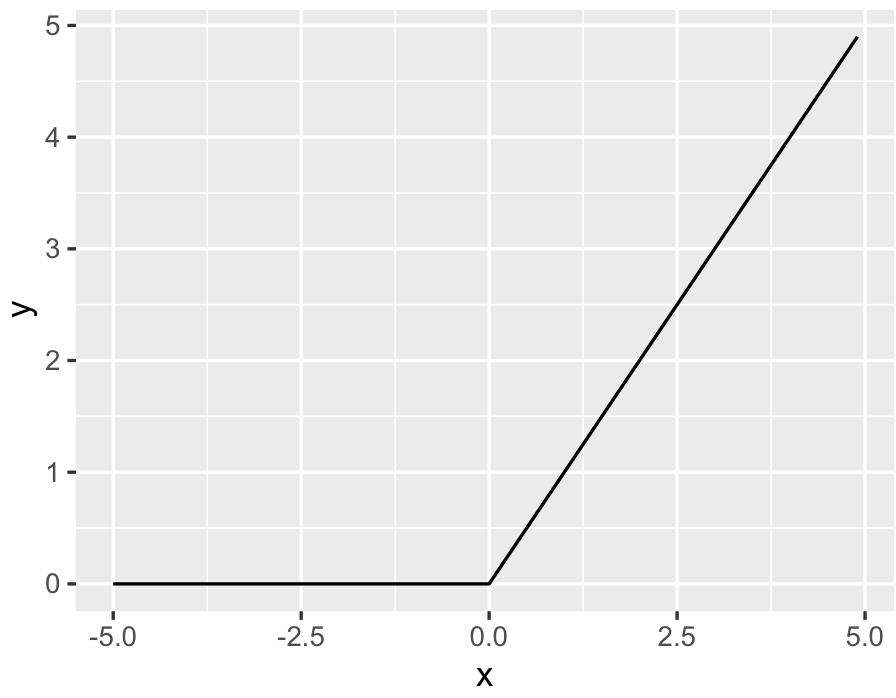
3. 소프트맥스(Softmax) 함수

소프트 맥스 함수는 활성화 함수 중에서도 출력층에서 사용하는 활성화 함수입니다.
소프트 맥스 함수는 결과 값에 대해 0에서~1 사이의 값으로 변환해 주는 역할만 할 뿐, 결과가 바뀌는 등의 영향을 미치지는 않습니다.
결과에 영향을 미치지 않아 실제 추록 과정에서는 사용하지 않지만, 학습 단계에서 영향도를 확인하는 척도로 사용합니다.
소프트 맥스 함수식은 다음과 같습니다.

함수식을 조금 살펴보면, 분모는 모든 입력값(a)의 지수함수에 대한 총합이고 분자는 입력값(a)의 지수함수입니다.
이 식을 파이썬에서는 아래와 같이 구현합니다.

1
2
3
4
5
6
7
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a-c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

exp_a는 소프트맥스 함수 식에 없는 처리를 하고 있는데, 입력값 중(a) 최대값(c)를 구한 후 최대값(c)을 일괄적으로 뺀 지수함수를 구하고 있습니다. 이같은 처리를 하는 이유는 지수함수의 특징 때문입니다.
지수함수는 쉽게 큰 값을 출력합니다. 이 때는 숫자 값이 아닌 무한대를 뜻하는 inf값을 출력하게 됩니다.
이 문제를 방지하고자 최댓값을 빼는 것이 일반적입니다. 지수 함수는 일괄적으로 더하거나 빼도 결과가 바뀌지 않습니다.

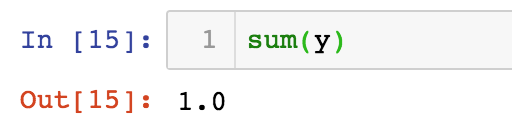
결과는 다음과 같습니다.

1
2
3
4
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)

print(y)

소프트 맥스 함수는 결과 값의 합이 항상 1인 것이 특징입니다.

R에서도 마찬가지로 최댓값을 빼는 방법으로 소프트맥스 함수를 구현합니다.

1
2
3
4
5
6
softmax <- function(a)
{
    exp_a <- exp(a - max(a))
    sum_exp_a <- sum(exp_a)
    return(exp_a / sum_exp_a)
}

4. 교차 엔트로피 오차 함수

교차 엔트로피 오차 함수는 손실함수에 사용하는 함수이다. 딥러닝 학습 시에 손실함수를 최소화하는 매개변수를 찾는 것을 목표로 한다.
교차 엔트로피 오차 식은 다음과 같다.

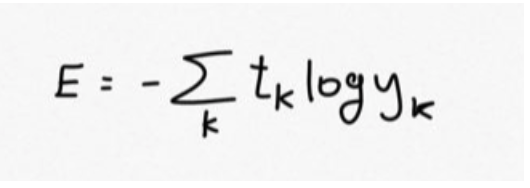
파이썬으로 다음과 같이 구현한다.

1
2
3
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

delta변수 역시 소프트맥스 함수와 비슷한 이유로 추가했는데, np.log() 함수에 0을 입력하면 마이너스 무한대를 뜻하는 -inf가 출력됩니다. 이문제를 방지하기 위해 아주 작은 값인 delta를 추가하게 됩니다.

교차엔트로피 오차는 다음과 같은 값을 출력합니다.

1
2
3
4
t = [0,0,1,0,0,0,0,0,0,0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]

cross_entropy_error(np.array(y), np.array(t))
1
2
3
4
t = [0,0,1,0,0,0,0,0,0,0]
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]

cross_entropy_error(np.array(y), np.array(t))

설명하면, t는 정답 레이블이고 y는 예측값입니다. 예측 값(y)을 정답레이블(t)로 채점하고 얼마나 틀렸나 확인해주는 것입니다. 첫번째 t에서 정답은 3번째=1)입니다. 그리고 y는 3번째가 정답일 확률을 0.6이라고 나타낸 것입니다. 이 때의 교차 엔트로피 오차값은 0.51입니다. 반면, 두번째와 같이 t에서 정답이 3번째(=1)인데, y는 3번째가 정답일 확률을 0.1로 나타냈더니, 교차 엔트로피 오차값은 2.30이 되었습니다. 정리하면, 오차율이 낮을 수록 교차 엔트로피 오차값이 낮아지며, 오차값이 낮을 수록 정확도가 높다는 것을 의미하게됩니다.

R에서는 다음과 같이 구현합니다.

1
2
3
4
cross_entropy_error_single <- function(y, t) 
{
    return(-sum(t*log(y+1e-7)))
}

마찬가지로 파이썬과 같이 y와 t값을 넣어보면 같은 결과를 확인할 수 있습니다.

지금까지 딥러닝 함수에서 기본적으로 사용하는 함수들을 파이썬과 R로 구현해보며 살펴 보았습니다.
기본 함수에 있어서는 언어 표현 방식의 차이일 뿐 같은 방식으로 구현하는 것을 확인할 수 있었습니다:)

#

Comments

×